Matematikusok már régóta próbálkoznak végtelenül összetett, ismétlődő elemekből álló struktúrák térbeli ábrázolásával. A feladatnak a 70-es években még a számítási kapacitás volt a legnagyobb akadálya, amikoris Benoît Mandelbrot elsőként a 2 dimenziós fraktálok ábrázolásával fáradozott. A technika fejlődésével azonban lelkes matematikusok csoportja mára rutinfeladattá tette a 2D fraktálok alkotását, néhány egyszerű programmal bárki egyedi művet is létrehozhat.

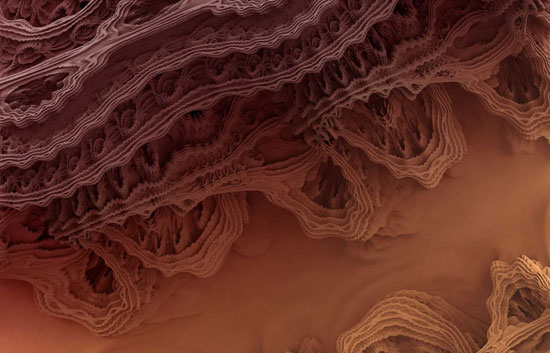
A következő áttörést a faktálok további dimenziókba való kiterjesztése jelenti, ebben alkotott most maradandót amatőr fraktálvadászok egy csoportja, akik megalkották az általuk "Mandelbulb"-nak nevezett alakzatot, ami mai ismeretieink szerint a legközelebb áll egy valódi 3D fraktálhoz:

Egy-egy ilyen forma valójában egyetlen matematikai képlettel leírható, többek között ettől is olyan nagyszerű. A bonyolult szerkezethez egy iteratív művelet eredményeként jutnak, azaz egy kiindulási számra végrehajtanak egy számítást, majd a kapott eredményre végrehajtják ugyanazt a számítást, és így tovább a végtelenségig. Ha a folyamatot  ábrázoljuk, akkor egyes esetekben gyönyörű alakzatokhoz juthatunk, ezek a fraktálok.

A számítás 3D-be való megjelenítése azonban eddig problémákba ütközött, ugyanis az eddig nem mutatott valódi végtelen részletességet. A most megalkotott formula még szintén tartalmaz "feltöltött" régiókat, melyek nem viselkednek valódi fraktálként, a teljes alakzat azonban még így is bámulatos részletességet mutat.

A Mandelbulb mellett más próbálkozások is vannak 3D (sőt 4D) fraktálok létrehozására, a képi megjelenítés mellett pedig több program hanggá is képes a műveletet alakítani. Mindemellett ilyen alakzatok a természetben is megfigyelhetők. A villám ágai is fraktálokként viselkednek, hasonlóan egyes levelek erezetéhez, felhők alakjához,  hegycsúcsok kőcsipkéihez vagy éppen a humán genom sejtmagban elfoglalt szerkezetéhez.

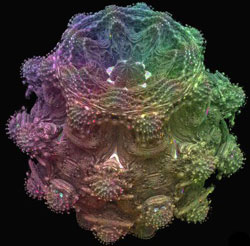A bejegyzésben szereplő képek mind a Mandelbulbról készültek, különböző oldalairól vagy üregeiről, más-más nagyítással. A teljes struktúra valójában a lenti képleten alapul és jobboldali képen látható teljes nagyságában.

{x,y,z}^n = r^n {cos(n*theta) cos(n*phi), sin(n*theta)cos(n*phi), -sin(n*phi)}
r=sqrt(x²+y²+z²), theta=atan(y/x), phi=atan(z/sqrt(x²+y²))

forrás:
Skytopia
Paul Nylander
New Scientist